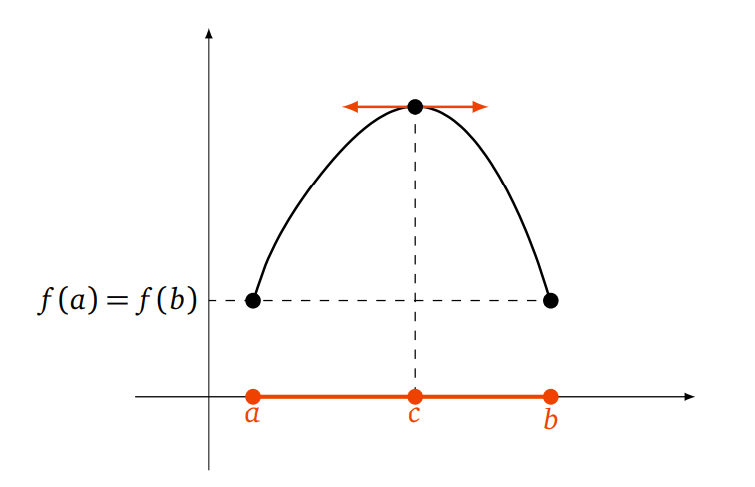
Montrez que si \(f:[a,b]\to{\Bbb R}\) est continue sur \([a,b]\) et dérivable sur \(]a,b[\), et si \(f(a)=f(b)\), alors $$\exists c\in]a,b[,\quad f^\prime(c)=0$$ (théorème de Rolle)

Continuité \(\to\) existence de min et max global
Comme \(f:[a,b]\to{\Bbb R}\) est continue sur \([a,b]\), alors elle admet un maximum global et un minimum global : $$\exists x_0,x_1\in[a,b],\forall x\in[a,b],\quad f(x_0)\leqslant f(x)\leqslant f(x_1)$$

La dérivée d'un extremum global qui n'est pas une borne de l'intervalle est nulle
Comme \(x_0\) et \(x_1\) sont des extremums locaux, on a : $$\begin{align} x_0\in]a,b[&\implies f^\prime(x_0)=0\\ x_1\in]a,b[&\implies f^\prime(x_1)=0\end{align}$$

\(x_0,x_1\in\{a,b\}\implies f(x_0)=f(x_1)\) d'après la troisième condition du théorème

Alors \(f\) est constante sur \([a,b]\) et \(\forall x\in]a,b[,f^\prime(x)=0\)

(Continuité, Minimum global, Maximum global, Extremum global, Fonction constante)

Montrer que l'équation $$\sin x=x$$ admet une unique solution dans \([0,\frac\pi2]\)

Pour \(x=0\), on a \(\sin x=0\), donc \(0\) est une solution de l'équation
Montrons que c'est la seule solution

Par l'absurde, si deux solutions, appliquer le théorème de Rolle

Par l'absurde, supposons que l'équation possède deux solutions dans \([0,\frac\pi2]\)
Alors, il existe deux réels \(x_1,x_2\in[0,\frac\pi2]\) tels que \(f(x)=\sin x-x =0\)
D'après le théorème de Rolle, on a donc : $$\begin{align}&f^\prime(x)=0\\ \implies&\cos x-1=0\\ \implies&\cos x=1\\ \implies&x=\arccos(1)\\ \implies&x=-\frac\pi2\notin\left[0,\frac\pi2\right]\end{align}$$
C'est absurde, donc l'équation \(\sin x=x\) admet une unique solution sur \([0,\frac\pi2]\)

(Sinus, Arccosinus)